排序算法总结

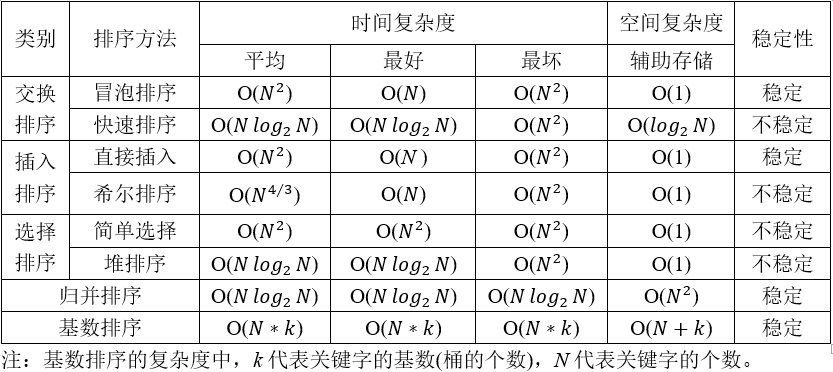
排序算法说明

涉及到的术语

稳定性：若两个数相等，排序后两个数的先后顺序没有改变，则稳定，否则不稳定。
内排序：所有排序操作都是在内存中完成。
外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行。

交换排序之冒泡排序

算法思想

比较相邻俩个数的大小，若大小顺序有误，则交换两数；每次遍历都会把最大（小）的数移动到尾（首）。

演示动图

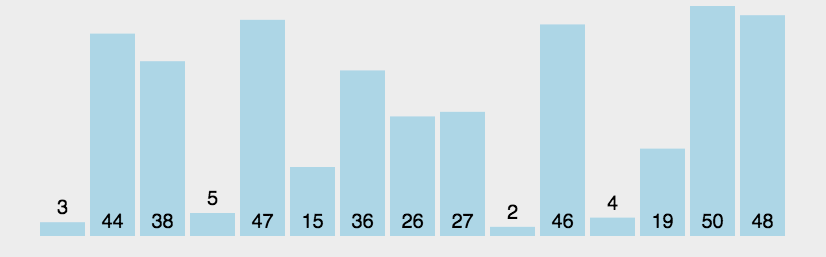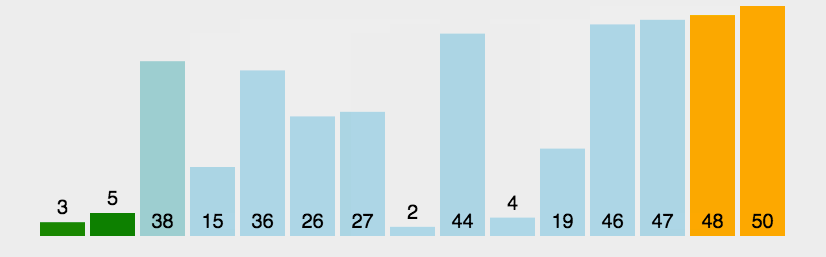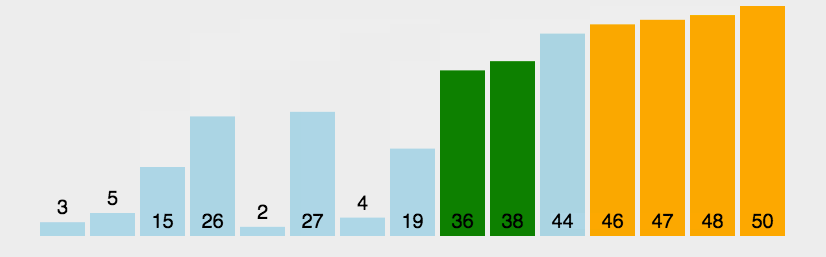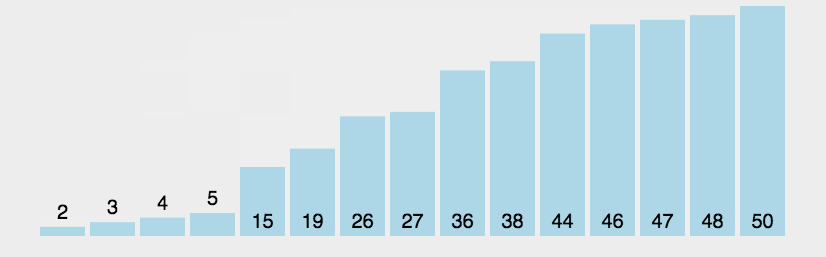
bubbleSort

算法实现

private static void bubbleSort(int[] sums) {
    for (int i = 0; i < sums.length - 1; i++) {
        boolean tag = true; 
        // 优化算法，若有一趟排序种，没有任何数据进行交换，说明数列已经有序
        for (int j = 0; j < sums.length - i - 1; j++) {
            if (sums[j] > sums[j + 1]) {
                int temp = sums[j];
                sums[j] = sums[j + 1];
                sums[j + 1] = temp;
                tag = false;
            }
        }
        if (tag)
            return;
    }
}

算法分析

时间复杂度：最好的情况是原序列为有序，需要比较（N-1）次；最坏情况是原序列是反序，需要进行（N-1）趟排序，每趟排序需要比较（N-i）次，故时间复杂度为O( $N^2$ )，平均时间复杂度为O( $N^2$ )。
空间复杂度：O(1)。
稳定。

交换排序之快速排序

算法思想

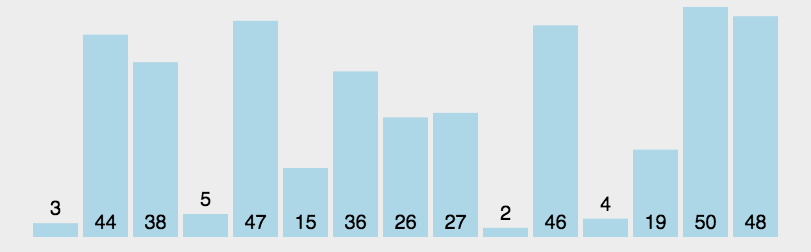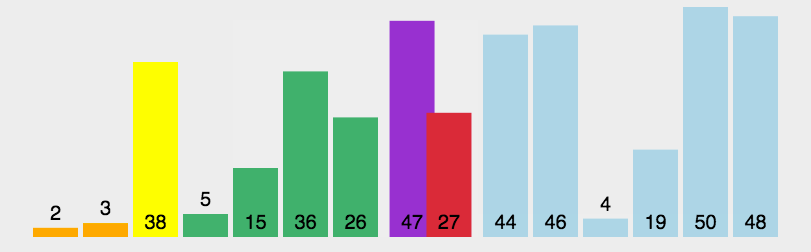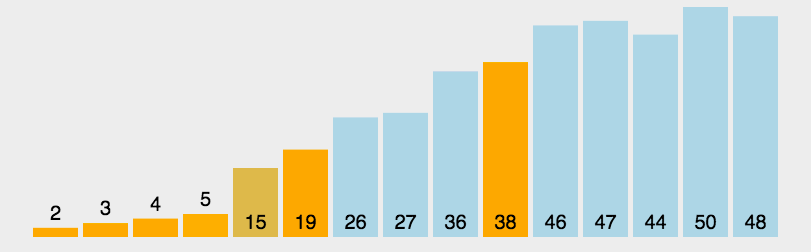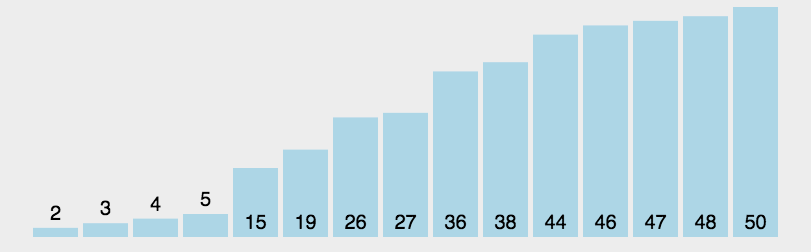
分治法，通过一趟排序将数列分成两个独立的部分，选取一个基准值，将小于基准值的数移动到基准值左边，大于基准值的数移动到基准值的右边。整个排序过程可以递归进行，使得整个序列有序。

演示动图

quickSort

算法实现

private static int[] quickSort(int[] nums, int low, int high) {
    int pivot = nums[low];
    int i = low;
    int j = high;
    while (i < j) {
        while ((i < j) && (nums[j] > pivot)) {
            j--;
        }
        while ((i < j) && (nums[i] < pivot)) {
            i++;
        }
        if (i == j) break;
        if ((nums[i] == nums[j]) && (i < j)) { // nums[i]=nums[j]=pivot
            i++;
        } else { // 也保证了基准值在序列的最后
            int temp = nums[i];
            nums[i] = nums[j];
            nums[j] = temp;
        }
    }
    if (i - 1 > low) nums = quickSort(nums, low, i - 1);
    if (j + 1 < high) nums = quickSort(nums, j + 1, high);
    return nums;
}

算法分析

时间复杂度：一次划分算法从两头交替搜索，直到 low 和 high 重合，其时间复杂度为O(N)；整个算法的时间复杂度与划分的次数有关。最好的情况每次划分所选择的基准值几乎将当前序列等分，经过 $log_2N$ 次划分，便可以得到长度为1的子序列，整个算法的时间复杂度为O( N $log_2N$ )；最坏情况每次划分所选的基准值恰好为当前序列中的最大或最小值，使得每次划分得到的子序列中一个为空，一个为其长度为原序列的长度-1。长度为N的序列需要经过N趟划分，使得整个排序算法的时间复杂度为O( $N^2$ )。平均时间复杂度为O(N $log_2N$ )。
空间复杂度：需要一个栈空间来实现递归，最好情况，所需栈的最大深度为 $log_2(N+1)$ ；最坏情况，所需栈的最大深度为 N 。故其空间复杂度为 $log_2N$ 。
不稳定。

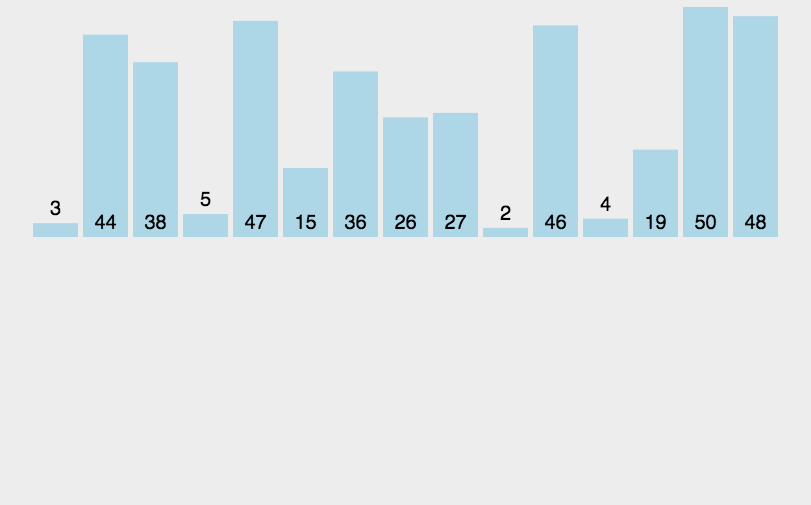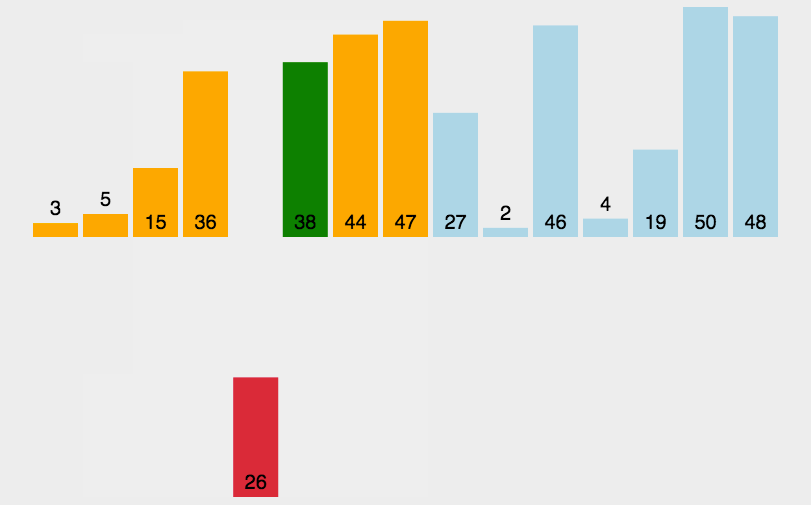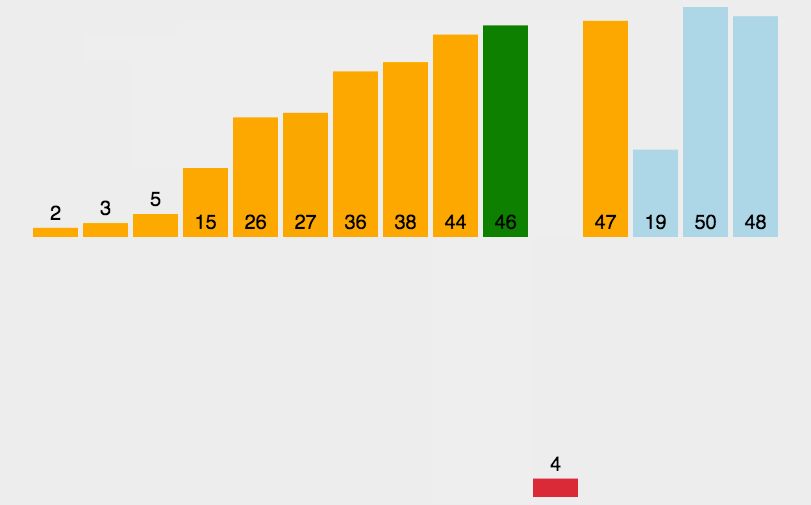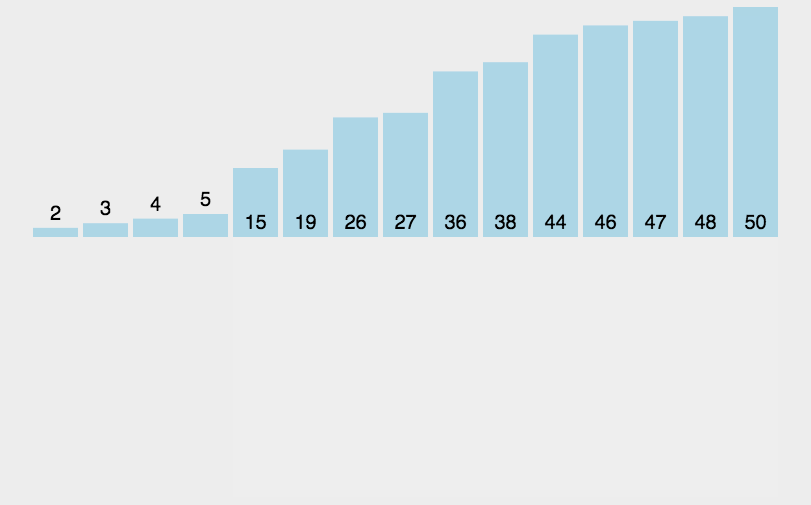
插入排序之直接插入排序

算法思想

每一趟将一个待排序的记录，按其大小插入到已经排序号的一组记录的适当的位置上，直到所有的数据都插入为止。

演示动图

insertSort

算法实现

private static int[] insertSort(int[] nums) {
    for (int i = 1; i < nums.length; i++) { // 第0位数左右有序的序列
        // 0~i-1位为有序，若第i位小于i-1位，继续寻位并插入，否则认为0~i位也是有序的，忽略此次循环
        if (nums[i] < nums[i - 1]) { 
            int curr = nums[i];
            int prev = i - 1;
            // 从第i-1位开始向前遍历并移位，直到找到比当前值小的位置。
            while (prev >= 0 && curr < nums[prev]) { 
                nums[prev + 1] = nums[prev];
                prev--;
            }
            nums[prev + 1] = curr;
        }
    }
}

算法分析

时间复杂度：共需要N-1趟排序，最好情况，原序列就有序，每趟排序只需要比较1次，数据不需要移动，时间复杂度为O( N )；最差情况，原序列为反序，第 i 趟排序需要比较（i+1）次，数据需要移动 i 次，整个算法比较的次数为 $\frac{(N-1)*(2+N)}{2}$ ，移动的次数为 $\frac{(N-1)*N}{2}$ ，所以时间复杂度为O( $N^2$ )。算法平均时间复杂度为O( $N^2$ )。
空间复杂度：O(1)。
稳定。

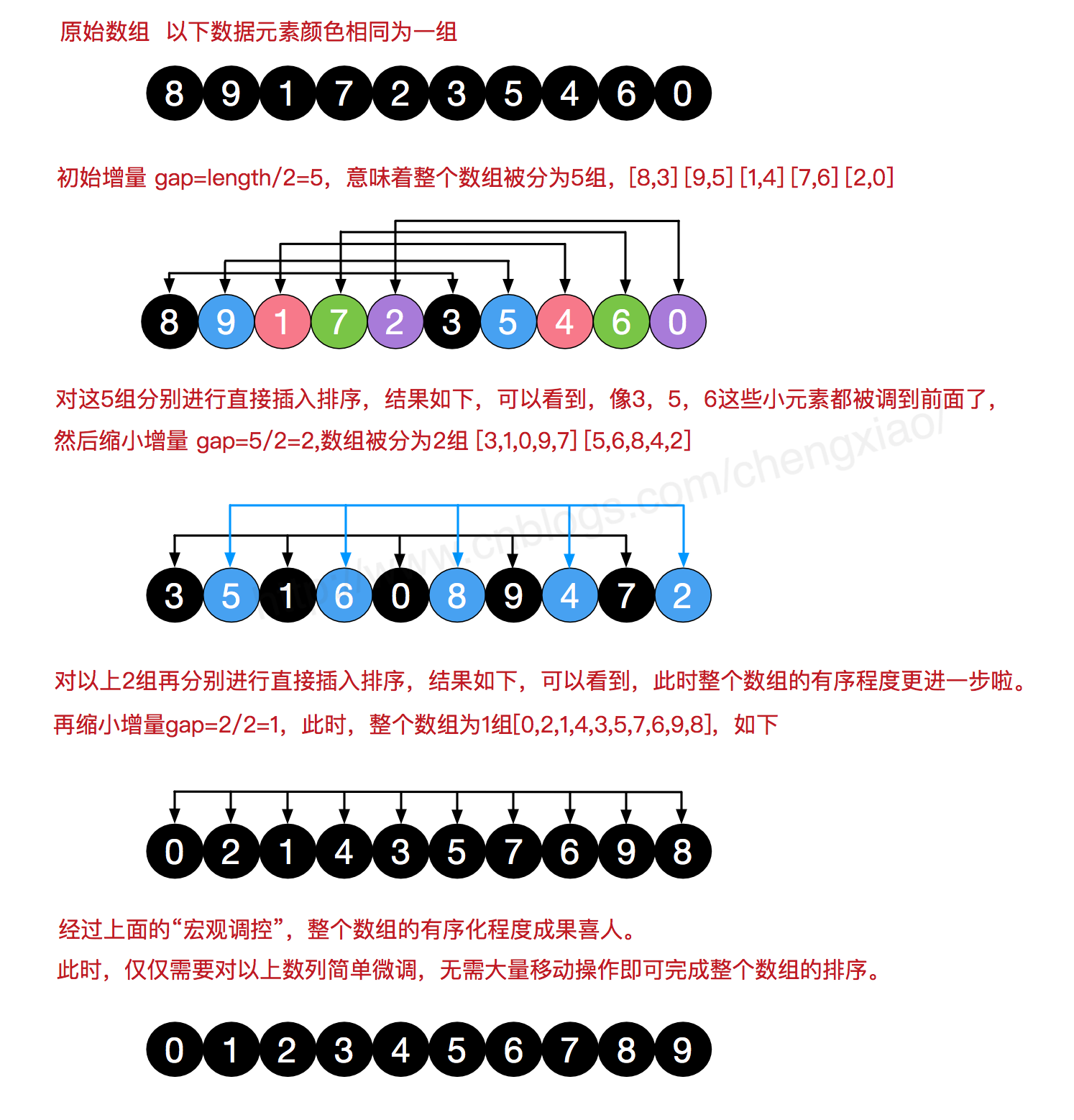
插入排序之希尔排序

算法思想

选取一个整数作为增量（一般为 $d_1=length/2$ ），所以距离的为增量 $d_1$ 的数为一组，先在各个组内进行直接插入排序，再取第二个增量 $d_2=d_1/2$ 重复上述分组与排序，直到所取的增量 $d_t=1$ ，即所有记录放在同一组中进行分组直接插入排序。

过程演示

ShellSort

算法实现

private static void shellSort(int[] nums) {
    int d = nums.length;
    do {
        d = d / 2;
        for (int i = 0; i < d; i++) {
            for (int j = i + d; j < nums.length; j += d) {
                int curr = nums[j];
                int prev = j - d;
                while (prev >= 0 && curr < nums[prev]) {
                    nums[prev + d] = nums[prev];
                    prev -= d;
                }
                nums[prev + d] = curr;
            }
        }
    } while (d != 1);
}

算法分析

时间复杂度：O( $N^\frac{4}{3}$ )
空间复杂度：O(1)
不稳定
与直接插入排序算法先比较，减少了移动次数，速度要跟快。原因：当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。
中等大小规模表现良好，对规模非常大的数据排序不是最优选择。

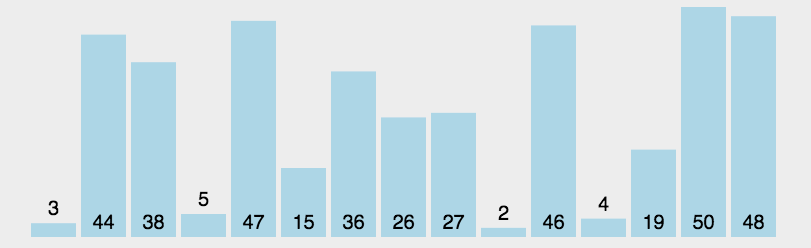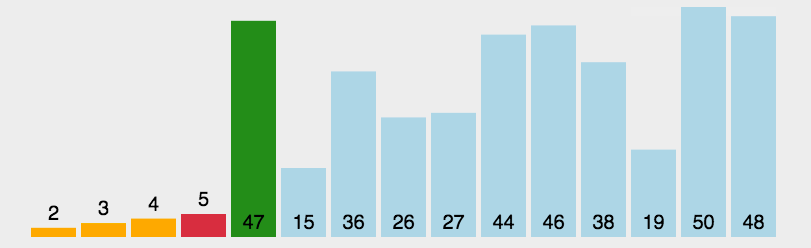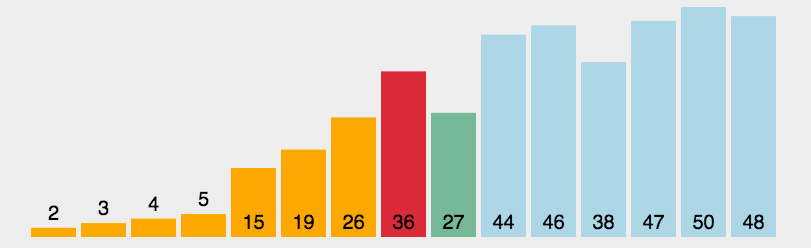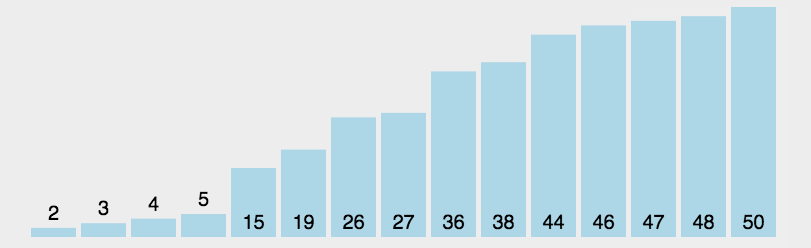
选择排序之简单选择排序

算法思想

首先从未排序的序列中找到最小的元素放在已排序的序列的起始位置，再在剩下的未排序元素中找到最小的元素放在已排序序列的尾部，以此类推，直到序列完全有序。

动图演示

sectionSort

private static void sectionSort(int[] nums){
    for (int i = 0; i < nums.length; i++) {
        int minIndex = i;
        for (int j = i+1; j < nums.length; j++) {
            if (nums[j]<nums[minIndex]){
                minIndex = j;
            }
        }
        if (minIndex != i){
            int temp = nums[i];
            nums[i] = nums[minIndex];
            nums[minIndex] = temp;
        }
    }
}

算法分析

时间复杂度：最好情况为O(N)，最坏情况为O( $n^2$ )，平均时间复杂度为O( $n^2$ )
空间复杂度：O(1)
稳定

选择排序之堆排序

算法思想

    堆排序首先将序列生成大顶堆（小顶堆），此时序列中最大的元素就在堆顶（完全二叉树的根节点），将堆顶元素与最后一个节点值交换，再将交换后的完全二叉树调整成堆，重复上述操作，直至序列完全有序。
堆的定义：
    1）完全二叉树：除了最后一层之外的其他每一层都被完全填充，并且是从左往右填充。
    2）大顶堆：父节点的值 > = 子节点的值；小顶堆：父节点的值 < = 子节点的值
由于完全二叉树节点连续，中间无断裂，故可以一维数组表示完全二叉树。第 i 个节点的父节点的索引为 $parent = (i-1)/2$ ，左子节点的索引为 $leftChild=2*i+1$ ，右子节点索引为 $rightChild=2*i+2$ 。

动图演示

HeapSort

算法实现

private static int[] heapSort(int[] nums) {
    // 将序列构建成堆
    int lastNode = nums.length - 1;
    int lastParent = (lastNode - 1) / 2;
    // 从最后一个父节点开始计算
    for (int i = lastParent; i >= 0; i--) {
        adjustHeap(nums, nums.length, i);
    }
    // 上述堆已经构建完成，开始排序
    for (int i = nums.length - 1; i > 0; i--) {
        // 元素交换,去掉大顶堆
        // 把大顶堆的根元素，放到数组的最后；
        swap(nums, 0, i);
        // 接下来我们需要排序的，就是已经去掉了部分元素的堆了
        adjustHeap(nums, i, 0);
    }
    return nums;
}
/**
 * 堆排序最关键的地方，调整二叉树，使其满足堆的要求
 *
 * @param nums   待组堆
 * @param length 堆的长度
 * @param i      堆的起始节点
 */
private static void adjustHeap(int[] nums, int length, int i) {
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;
    int max = i;
    if ((leftChild < length) && nums[leftChild] > nums[max]) {
        max = leftChild;
    }
    if ((rightChild < length) && nums[rightChild] > nums[max]) {
        max = rightChild;
    }
    if (max != i) {
        swap(nums, i, max);
        // 递归调整发生交换后的堆
        adjustHeap(nums, length, max);
    }
}
private static void swap(int[] nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

算法分析

时间复杂度：在构建堆的过程中，是从完全二叉树最下层的非叶子节点开始构建的，将它和其孩子节点进行比较和有必要的交换，对于每个非叶子节点，最多2次比较和交换，故初始化堆的时间复杂度为O(N)。在正式排序时，第i 次取堆顶元素和重建堆需要的时间复杂度为O( $log_2i$ )，(完全二叉树的某个节点到根节点的距离为 $log_2i -1$ )，需要取 $N-1$ 次栈顶元素，故重建堆的时间复杂度为O( $Nlog_2N$ )。由于堆排序对元素记录的排序状态不敏感，因此它无论最好，最坏，和平均时间复杂度均为O( $Nlog_2N$ )。
空间复杂度：O(1)。
不稳地

归并排序

算法思想

采用分治法，利用递归与分治技术将数据序列划分成为越来越小的子序列，之后对子序列排序，最后再用递归方法将排好序的子序列合并成为有序序列。
1) 把长度为n的输入序列分成两个长度为n/2的子序列；
2) 对着两个子序列使用归并排序（递归调用）；
3）将排序好的两个子序列合并得到最终的有序序列。

动图演示

mergeSort

算法实现

private static int[] mergeSort(int[] nums) {
    if (nums.length < 2)
        return nums;
    int mid = nums.length / 2;
    int[] left = Arrays.copyOfRange(nums, 0, mid);
    int[] right = Arrays.copyOfRange(nums, mid, nums.length);
    return merge(mergeSort(left), mergeSort(right));
}
/**
 * 将两个有序子序列合并成一个有序序列
 */
private static int[] merge(int[] left, int[] right) {
    int[] result = new int[left.length + right.length];
    for (int i = 0; i < result.length; i++) {
        int leftIndex = 0;
        int rightIndex = 0;
        if (leftIndex >= left.length)
            result[i] = right[rightIndex++];
        else if (rightIndex >= right.length)
            result[i] = left[leftIndex++];
        else if (left[leftIndex] <= right[rightIndex])
            result[i] = left[leftIndex++];
        else
            result[i] = right[rightIndex++];
    }
    return result;
}

算法分析

时间复杂度：最好的情况O(N)，最差的情况O( $Nlog_2N$ )，平均时间复杂度O( $Nlog_2N$ )。
空间复杂度：O( $N$ )
稳定

基数排序

算法思想

非比较排序，将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

演示动图

radixSort

算法实现

private static int[] radixSort(int[] nums) {
    if (nums == null || nums.length < 2)
        return nums;
    // 计算最大数的位数
    int max = nums[0];
    for (int i = 1; i < nums.length; i++) {
        max = Math.max(nums[i], max);
    }
    int maxCount = 0;
    while (max != 0) {
        max /= 10;
        maxCount++;
    }
    // 创建10个桶
    List<List<Integer>> bucketList = new ArrayList<>();
    for (int i = 0; i < 10; i++) {
        bucketList.add(new ArrayList<>());
    }
    // 为了得到对应位的数值，mod去除高位，div去除低位
    int mod = 10, div = 1;
    for (int i = 0; i < maxCount; i++) {
        for (int num : nums) {
            int value = (num % mod) / div;
            bucketList.get(value).add(num);
        }
        // 每按照某一位排序都需要将数组索引还原为0
        int index = 0;
        for (List<Integer> aBucketList : bucketList) {
            for (Integer num : aBucketList) {
                nums[index++] = num;
            }
            aBucketList.clear();
        }
        mod *= 10;
        div *= 10;
    }
    return nums;
}

算法分析

时间复杂度：O( $N*k$ )
空间复杂度：O( $N+k$ )
稳定
算法总结
几种常用排序算法的算法性能如下图所示。